Graphe_Matrices
Matrice d‘incidence(关联矩阵)
Matrice d’incidence sommets-Arcs(有向图)
定义(顶点-弧的关联矩阵)
在图论中,关联矩阵(Matrice d’incidence) 是一种描述图中顶点与边(或弧)之间关系的矩阵。定义:
顶点-弧关联矩阵是一个矩阵,用于表示图中每个顶点与每个弧之间的关系。对于一个有向图或无向图的每个弧,矩阵中包含表示该弧和顶点之间的关联信息。
假设图有 n 个顶点和 m 条弧(边),则顶点-弧关联矩阵是一个 n \times m 的矩阵,其中:
- 每一行代表一个顶点(1,2,3,4)
- 每一列代表一个弧(或边)(a1,a2,a3…)
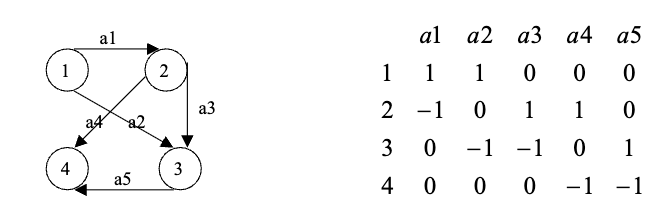
结构:
1 | typedef struct { |
Matrice d’incidence sommets-Arêtes(无向图)
无向图的顶点和边的关联矩阵

1 | typedef struct { |
sous forme condensée de la matrice d’incidence(关联矩阵的子表示形式)
a) colonne par colonne
On utilise deux tableaux α[] et β[] de dimension p=|A| donnant pour chaque arc ou arête a=1..p les numéros α[a] et β[a] des extrémités.
si G est orienté alorsα[a] est l’origine de a (α[a]存弧a的起点)β[a] est l’extrémité de a(β[a]存弧a的终点)
- 对于有向图
1 | //示例图 |
- 对于无向图
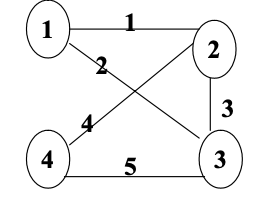
1 | α = [1, 1, 2, 2, 3] // 每条边的起点 |
1 | typedef struct{ |
b) ligne par ligne
有向图(Graphe orienté)
对于每个顶点
s:存储w⁺(s),即以s为起点的所有弧(即出边)。形式为:
1
w⁺(s) = { a | a = (s, t) ∈ A(G) }
例如,若
s = 1有两条出边(1, 2)和(1, 3),那么:1
w⁺(1) = { a₁, a₂ }
无向图(Graphe non-orienté)
对于每个顶点
s:存储w(s),即与s相关的所有边(即无向边)。形式为:
1
w(s) = { a | a = {s, t} ∈ A(G) }
例如,若
s = 2有两条关联边{1,2}和{2,3},那么:1
w(2) = { a₁, a₃ }
为了存储图的邻接信息,我们使用以下 3 个数组:
APS(Adresse Premier Successeur)
记录每个顶点的第一条边在
FS数组中的索引。类似于邻接表的起始索引。
需要引入虚拟顶点
n+1,其索引指向FS的终点,便于计算索引范围。
FS(File des Successeurs)
按顺序存储所有**边(或弧)**的索引。
该数组实际上是一个压缩后的邻接列表,但存储的是边的索引,而不是顶点。
AS(Adresses des Sommets)
存储
FS数组中每条边的终点(即目标顶点)。对于有向图,
AS[i]存储弧的终点t。对于无向图,
AS[i]存储边的另一个端点。
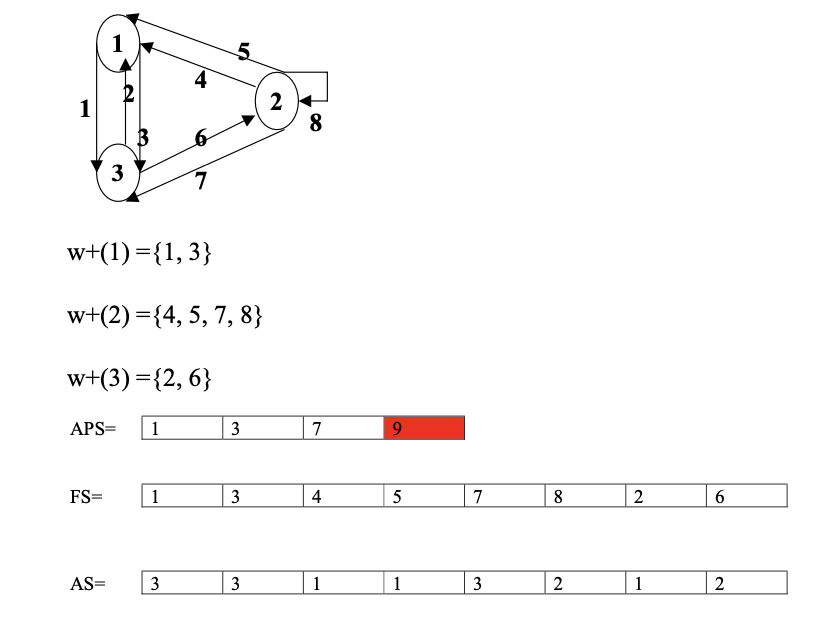
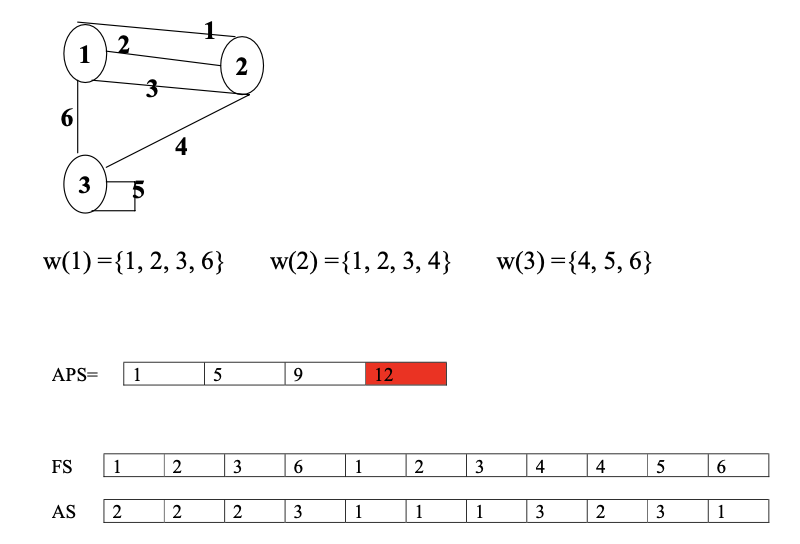
1 | typedef struct{ |
c) Listes d’incidences
- 有向图
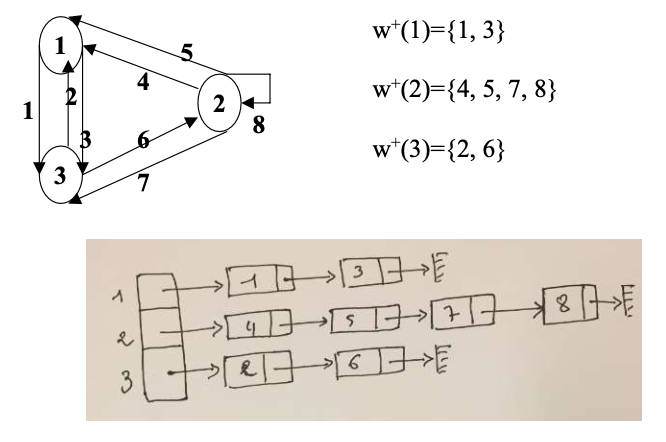
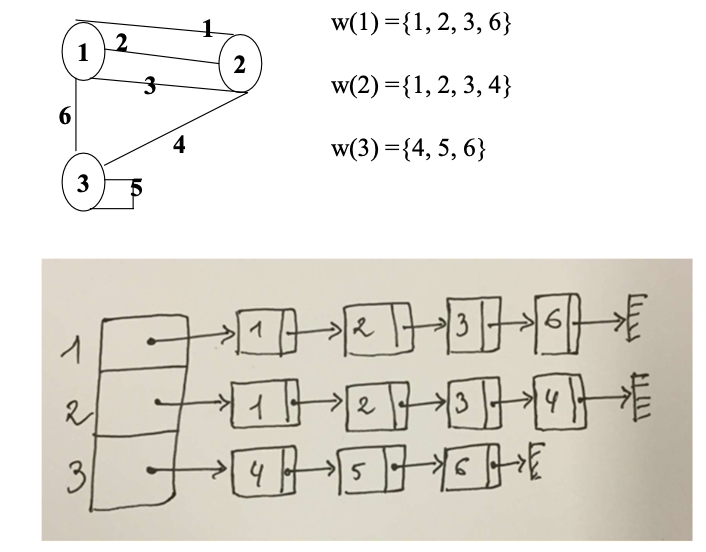
- 无向图
Matrices d’adjacence A(邻接矩阵)
1. 邻接矩阵的定义
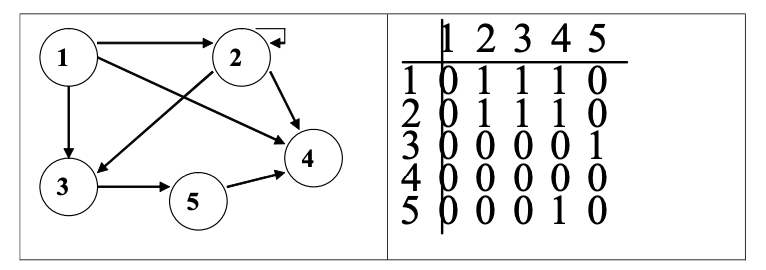
假设图中有 n 个顶点 S = {v1, v2, …, vn} ,则邻接矩阵是一个 n * n 的矩阵,矩阵中的元素 A[i][j] 表示顶点 vi 和顶点 vj 之间是否有边连接。
- 对于无向图,如果有边
(vi, vj),则A[i][j] = 1,否则A[i][j] = 0。 - 对于有向图,如果有弧从
vi指向vj,则A[i][j] = 1,否则A[i][j] = 0。 - 如果图包含自环(即一个顶点与自己相连),则在矩阵的对角线上
A[i][i] = 1。 - 有向图
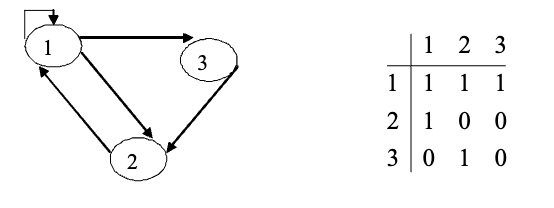
- 无向图
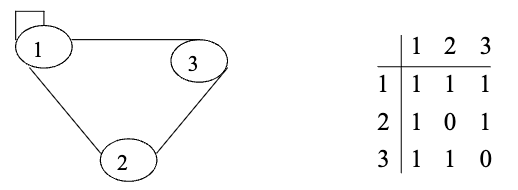
1 | ///Matrices d’adjacence A (邻接矩阵,表述顶点和顶点之间关系) |
2. Représentations des graphes(关联矩阵 VS 邻接矩阵)
图的表示方法:
- 邻接矩阵(Matrice d’adjacence)或其派生形式:
这种表示方法侧重于图是由一组顶点组成的。它适用于顶点集合固定不变的图(即图中的顶点不发生变化)。这种方法通过矩阵的形式表示顶点之间的连接关系,通常用于存储和处理稠密图(即边多的图)。 - 关联矩阵(Matrice d’incidence)或其派生形式:
这种表示方法侧重于图是由一组边(或弧)组成的。与邻接矩阵不同,关联矩阵通过矩阵表示图中的边及其与顶点的关联。它更适用于边集合固定不变的图,并且通常用于存储和处理稀疏图(即边少的图)。
总结:
- 邻接矩阵强调图的顶点,适合顶点数量固定的图。
- 关联矩阵强调图的边(或弧),适合边数量固定的图。
3. sous forme condensée de la matrice d’adjacence(邻接矩阵的子表示形式)
a) 后继队列(File des successeurs)
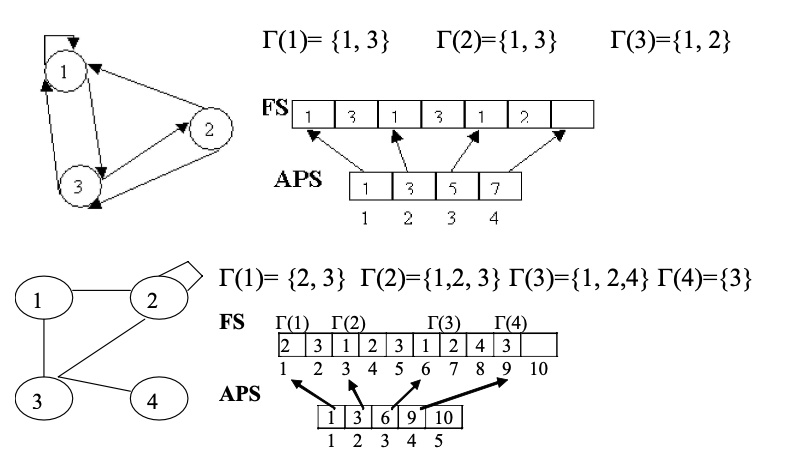
FS = File des successeurs
est un tableau linéaire contenant successivement les listes nonAPS = Adresse (=indice) du premier successeur
Tableau linéaire indicé par les numéros des sommets
FS:后继队列,存放所有非空的后继列表T(1), T(2), T(3)...(就是按顺序存每个顶点的后继节点列表)
APS:后继地址表,APS[s]表示顶点s第一个后继在FS中的位置
虚拟顶点:为了简化计算和管理,引入一个虚拟顶点s = p + 1,在后续操作时APS[n+1]会被设定为一个特定值p + 1来帮助简化计算(处理边界问题等)
1 | ///后继队列 |
b) 邻接列表(Listes d’adjacence)
在邻接列表中,每个顶点都有一个对应的列表,列表中包含该顶点所有相邻的顶点(即与该顶点有边相连的顶点)。
- 对于无向图,每条边会在两个顶点的列表中都出现
- 对于有向图,边只会出现在起点的列表中
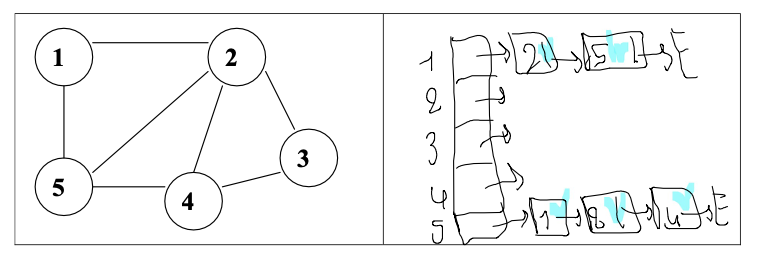
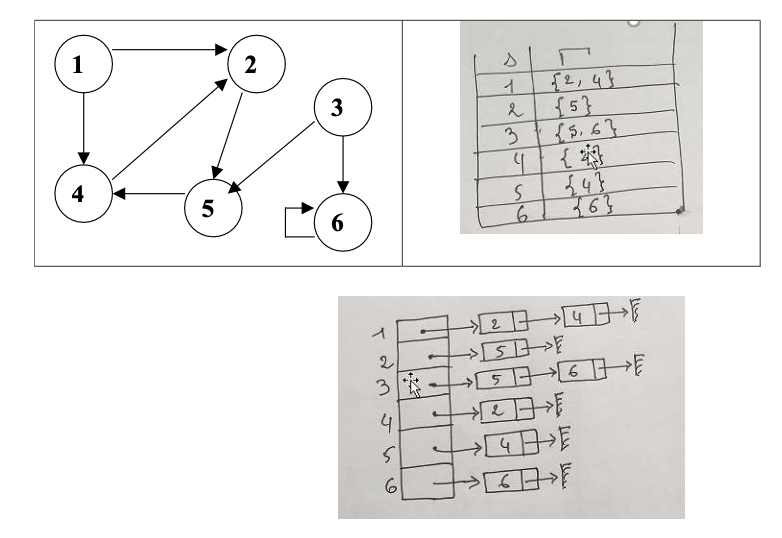
1 | ///邻接列表 |
c) 后继和前驱的列表数组(Tableau de listes successeurs et prédécesseurs)
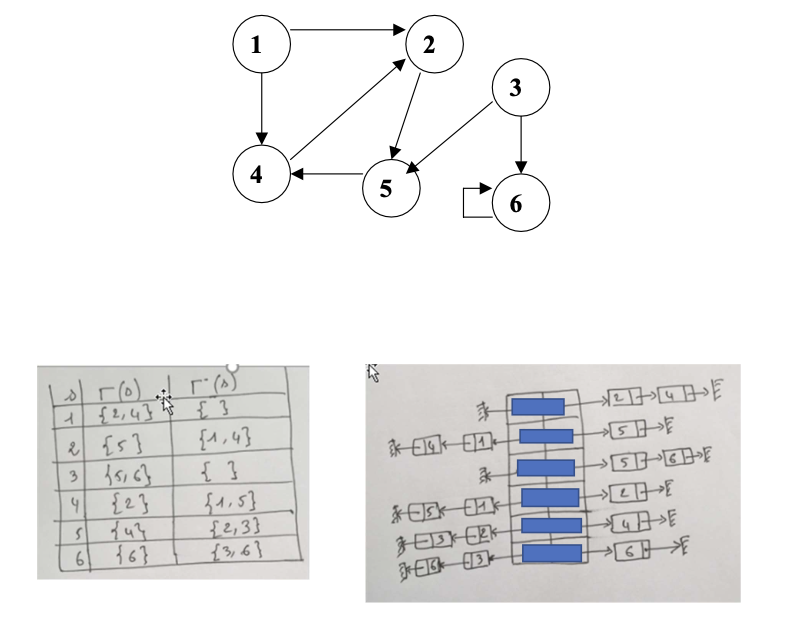
1 | //后继和前驱的列表 |
d) 主列表(Liste principale)
Les sommets du graphe sont associés en une liste linéaire appelée liste principale.
Chaque sommet du graphe étant représenté dans cette liste par une
structure comportant 3 membres :
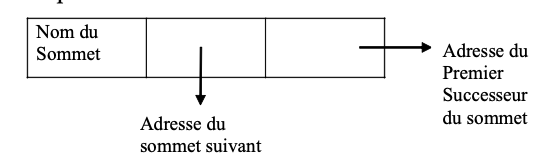
- Nom du sommet(顶点名称)
- Un pointeur sur le sommet suivant(下一个顶点)
- Un pointeur sur la liste des successeurs de ce sommet.(顶点的后继列表)
Chaque successeur t de s est représenté par une structure comportant 3 membres :
- Un pointeur vers la structure
tdans la liste principale - La valeur de l’arc
(s, t)dans le cas d’un graphe valué - Pointeur vers le sommet suivant de cette liste de successeurs
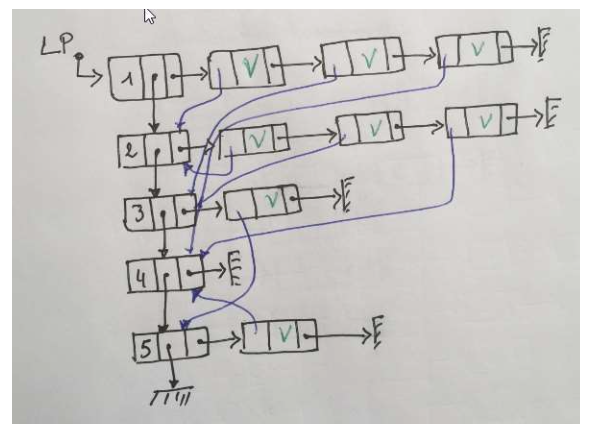
1 | //LP ListePrincipal |
e) 稀疏矩阵(Matrice creuse)
稀疏矩阵(Matrice creuse) 是指一个矩阵中大部分元素为零,或者非零元素所占的比例较低。通常,稀疏矩阵中的零元素非常多,因此我们不再存储这些零元素,而只存储非零元素。这样可以大大节省存储空间,并且提高计算效率。
稀疏矩阵的定义:
- 一个矩阵被称为稀疏矩阵,当矩阵中大部分元素为零,或者非零元素的比例较低。
- 在数学上,稀疏矩阵常见于大型数据结构中,例如图的邻接矩阵、有限元法的系数矩阵等。
稀疏矩阵的存储方式:
由于稀疏矩阵大多数元素为零,直接存储所有元素会浪费大量内存。因此,稀疏矩阵通常采用 指针表示法(Représentation dynamique par pointeur) 来存储,只保存非零元素及其位置。
方法一(矩阵的数学表示)
1
2
3
4
5
6
7
8
9
10
11
12
13
14typedef struct cellule {
int numlig; // 行号
int numcol; // 列号
TCout cout; // 存储矩阵元素的值
struct cellule *ligSuiv; // 指向同一行下一个元素的指针
struct cellule *colSuiv; // 指向同一列下一个元素的指针
}* Liste;
typedef struct matrice {
int nblig; // 行数
int nbcol; // 列数
Liste *ligne; // 每行的链表头指针
Liste *colonne; // 每列的链表头指针
} MatriceCreuse;方法二(图的表示)
1
2
3
4
5
6
7
8
9
10
11
12
13typedef struct cellule {
int somSucc; // 成功者(后继节点)
int somPred; // 前驱节点
TCout cout; // 存储边的权重或值
struct cellule *succSuiv; // 指向下一个成功者的指针
struct cellule *predSuiv; // 指向下一个前驱的指针
}* Liste;
typedef struct matrice {
int nbSom; // 顶点数(即图中的节点数)
Liste *tabSucc; // 每个节点的后继节点链表头指针
Liste *tabPred; // 每个节点的前驱节点链表头指针
} MatriceCreuse;





